Different types of Cost Functions in Deep Learning

March 01, 2022

In machine learning models, especially neural networks, the loss function is a function that informs us about the accuracy of our model predictions. It does so by calculating the difference between the values predicted by the model and the true values of the dataset. Predictive models can be used for different tasks, including binary classification, multi class classification and regression. Similarly different loss functions are used to calculate the losses for each of these prediction tasks. When plotting such loss functions, many local minima and saddle points are observed. Neural network models strive to find the best set of parameters to decrease the loss function.

Regression tasks

1. Mean Squared Error

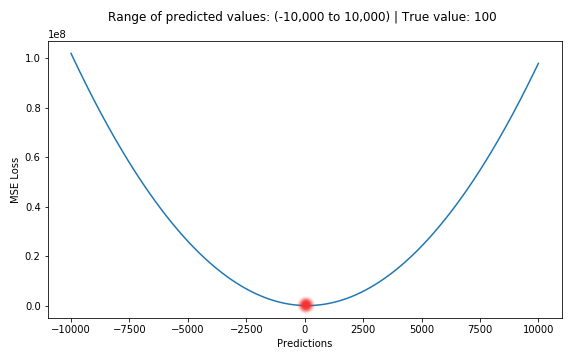
When dealing with Stochastic Gradient descent or any other optimization methods that update weights after every record, the squared error is given by, SE = $(y- \hat{y})^2$ . Here, $y$ is the real output value whereas $\hat{y}$ is our predicted output. When dealing with batch optimizers we use the mean squared error given by MSE = $\sum_{i=1}^t (y-\hat{y})^2$ where t is the batch size. As the mean squared and the squared errors are both quadratic functions, we notice a convex curve when plotting the function. The disadvantage of the MSE error function is it is not robust to outliers, i.e. if the dataset has some outliers the mean squared error will punish the error values of the outliers more because the square of the difference will be more. We can avoid this by using the absolute error loss.

2. Absolute Error Loss

Instead of squaring the difference we take the absolute value so that the error AEL= $\sum_{i=1}^t |y-\hat y|$ which is a linear equation. The advantage of this is that mean absolute error is more robust to outliers because the errors are not getting squared so we are not penalizing enough. However the computation of the absolute value is very difficult because we are using a modulus operator.

3. Huber Loss

Here we combine the two previous loss functions. The Huber error is written as, Loss = $\frac{1}{2} (y-\hat{y})^2$ if $|y-\hat{y}| \leq \delta$ otherwise, $Loss= \delta |y-\hat{y}| - \frac{1}{2} \delta^{2}$ (Linear eqn) where $\delta$ is a hyperparameter.

Classification tasks

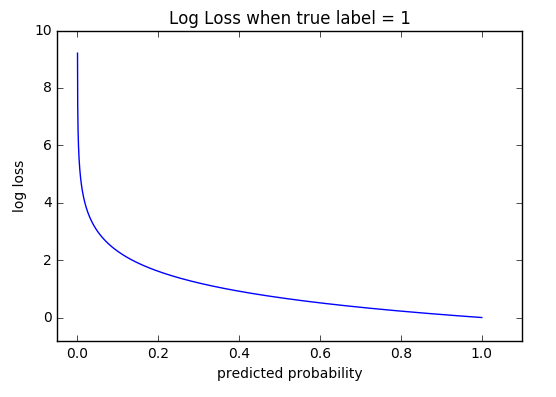
In Neural Networks, the outputs for classification tasks are probabilistic values, i.e. instead of providing the exact values similar to regression tasks, the output values y represent the probability that the input record belongs to a certain class. Hence, for an accurate model, the higher the probability of the output for the correct class, the better the performance and vice versa. Therefore our evaluation model should punish a lower output value for the actual class as this value corresponds to the prediction of the probability of the record belonging to that class being low. In the range of 0 to 1, the log function maps to exponentially high values for small valued inputs. Hence, it is used as the loss function to evaluate the performance of classification tasks.

1. Binary Cross Entropy

The binary cross entropy loss = $-y\log{}\hat{y} - (1-y)\log{}(1-\hat{y})$. Here, if the actual value y=0, Loss = $-\log{}(1-\hat{y})$ , otherwise if y=1, Loss = $-\log{}\hat{y}$. Here, y is found by using the sigmoid activation function where $\sigma = \frac{1}{1+e^{-z}}$, where z = $w^T X + b$ where X are the input values, w is the weight matrix and b is the bias . We consider that $\hat{y}$ denotes the probability of the particular record belonging to the positive class, i.e. y=1. Hence, if $\hat{y}$ is high, the model is predicting that the record belongs to class y=1. We can see that a high $\hat{y}$ value for y = 0 will correspond to $1-\hat{y}$ being small and hence, the Loss = $-\log{}(1-\hat{y})$ will be exponentially high.

2. Categorical Cross Entropy

For multi class classification problems, the output layer consists of c nodes where c= the number of classes in the problem and uses softmax as the activation function. For a particular record, the softmax function is given by:

$$\sigma(z_i) = \frac{e^z_i}{\sum_{j=1}^c (e^z_j)}$$

where i, j denote the nth node of the output layer. Usually, we use sigmoid for binary and softmax for multiclass classification. Hence, our neural network will have a vector output consisting of c items: $\hat{y_{ij}} = [\sigma(z_1) \sigma(z_2) \sigma(z_3) …… \sigma(z_c)]$ and each item will represent the probability of the record belonging to the class c. For multi class classification, we have to also remember to do one hot encoding on our target labels. One hot encoding will represent each category as a column and will represent the values of the columns as bits, where 1 denotes the record belongs to that categorical column and 0 denotes it does not. The target label will be a binary vector consisting of c items (the classes): $y_{ij} = [ class_1 \enspace class_2 \enspace class_3 \enspace ……. \enspace class_c ] \in [0,1]$ Hence, when dealing with Stochastic Gradient descent or any other optimization methods that update weights after every record,the categorical cross entropy loss is: $L(x_i , y_i) = - \sum_{j=1}^c y_{ij} \log{}(\hat{y_{ij}})$ When dealing with batch optimizers, the loss is given by: $L(x_i , y_i) = - \sum_{i=1}^t \sum_{j=1}^c y_{ij} \log{}(\hat{y_{ij}})$ , where t is the batch size Here, $y_i$ is a one-hot encoded target vector where i specifies the record or row number, i.e. $y_3$ denotes the target vector of record number 3. Hence, $y_{ij}$ denotes the jth item in the output vector of the ith record $( j \leq c)$.

---

Auras Khanal